Ways to calculate code performance
Approach 1: Time based approach
calculateTime()
function fancyName(){
do something
}
calculateTimeDifference()
In this approach of judging code, before running a chunk of code, the initial time is taken and after running that code, the final time is taken. Then when the final time is subtracted from initial time, we get the how much time was required for processing of the code.
This method of calculating code performance is rated as average but still this approach is used hugely to judge code
Problems in Approach 1:
- It is based on machine: Depends from processor to processor
- It is based on processing: Depends on the processing power of your PC
Approach 2:
Counting the number of operations in a code. Technically, this literally means that we are going to count the number of operations in a code.
Count Operation in the code below
a = a + 1
If you said there is one operation, you are wrong my friend. There are actually 2 operator: "=" and "+"
Now, count the operation in this code
sum = 0
winner = 1
for (i = 1; i < n; i++){
sum = sum+1
}
Notice closely, that there are several operators. In total, there is 3 "="s, 1 "<", then in i++, there are actually 2 operators which are responsible to increment the value of i, i++ can be written as i = i+1, so in i++ there are 2 operators. Then inside the loop there are 2 operators: "=" and "+"
But, in this code, apart from sum = 0, winner = 1, i=1, all the other operators are dependent on the variable n. So, there are 3 constant operators, and 5 operators which varies with the value of n. Thus there are 3+5n operators
Big O
The whole way of measuring code with number of operators is known as Big O.
Code 1
sum = 0
i = 0
while (i < n):
sum += i
i += 1
print(sum)
In this given code, there are 5n+2 operators.
Now, coming to the complexity of the code: To measure the complexity of the code, the constants are to be ignored.
So O(n) [Said as O of n] is the complexity
Code 2
for (------):
---------
---------
for (------):
---------
---------
You might think that the complexity of the above code is 2O(n) and that's completely correct. But since the constants are to be ignored, so the complexity will be O(n).
Code 3
for (let i = 0; i < N; i++) {
for (let j = 0; j < N; j++) {
sum+=j
}
}
In the above code, O(n) is inside another O(n). Thus, the complexity of the code becomes O(n^2). If the nested loop would run on a constant and not on N, the complexity would not be O(n^2).
Complexity Notation
| Code Complexity | Notation | Note |
| O(10), O(1000) O(k), 3O(k) kO(k) | O(1) | "k" is some constant |
| O(3n), O(4n+100000) | O(n) | Constants are to be ignored |
| O(3n^2), O(4n^2+100000) | O(n^2) | Constants are to be ignored |
| O(3n^2), O(4n^2 + 3n + 4) | O(n^2) | Since with increasing value of n, the value of n^2 will become much higher than theat of n, so n can be ignored, incase of cubic equations,the complexity will be O(n^3) and so on |
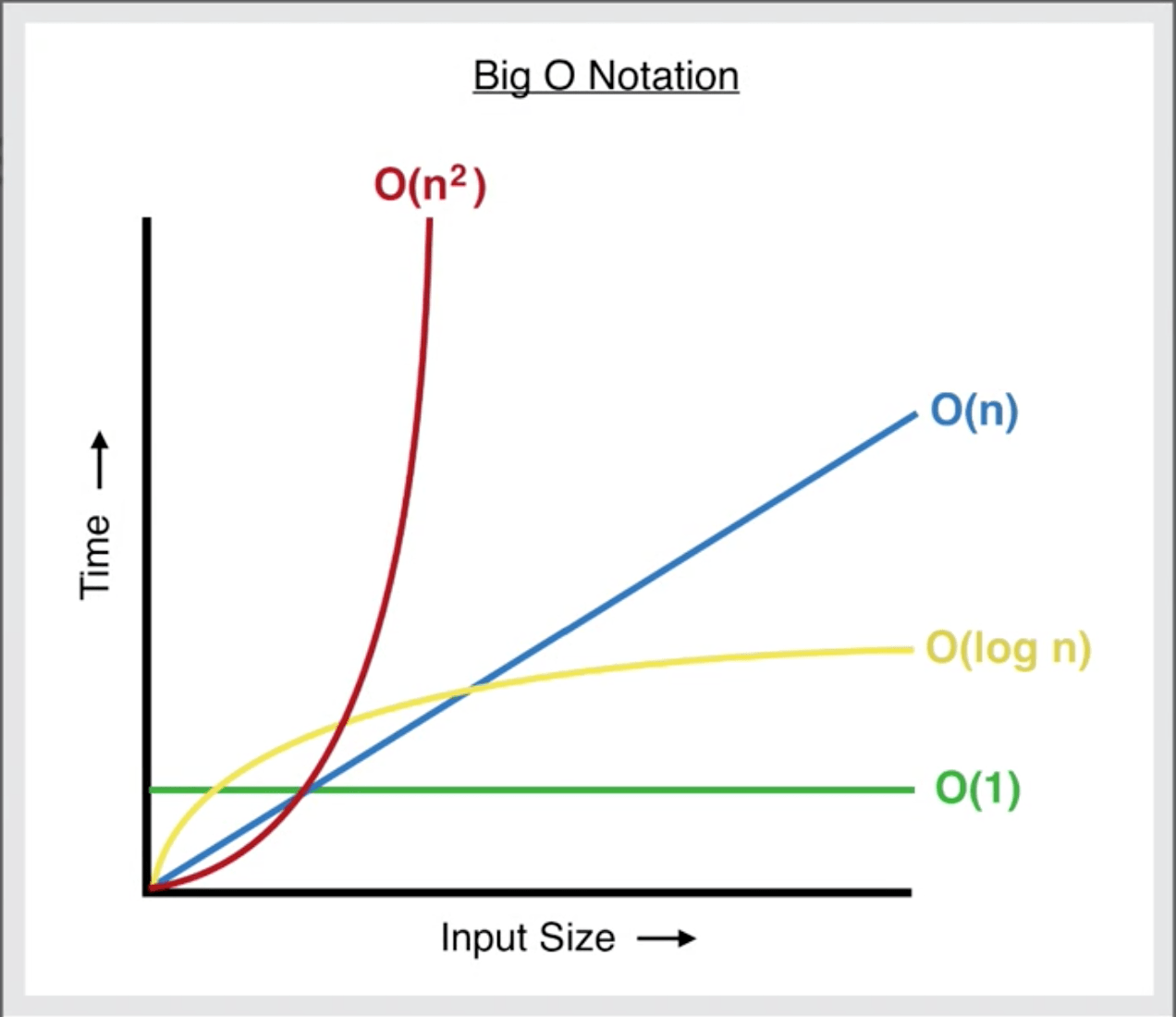
This graph shows the time for complexity of code with increasing input.
