If you are in this blog, you must know what Artificial Intelligence is so I am not going to waste time on those basic kinds of stuff. I would like to tell you some prerequisites before you dive deep into this article.

• You must know the fundamentals of programming i.e loops, functions, classes etc.

That's it. If you know that basic stuff, then its completely alright and you can follow along

Starting with an example

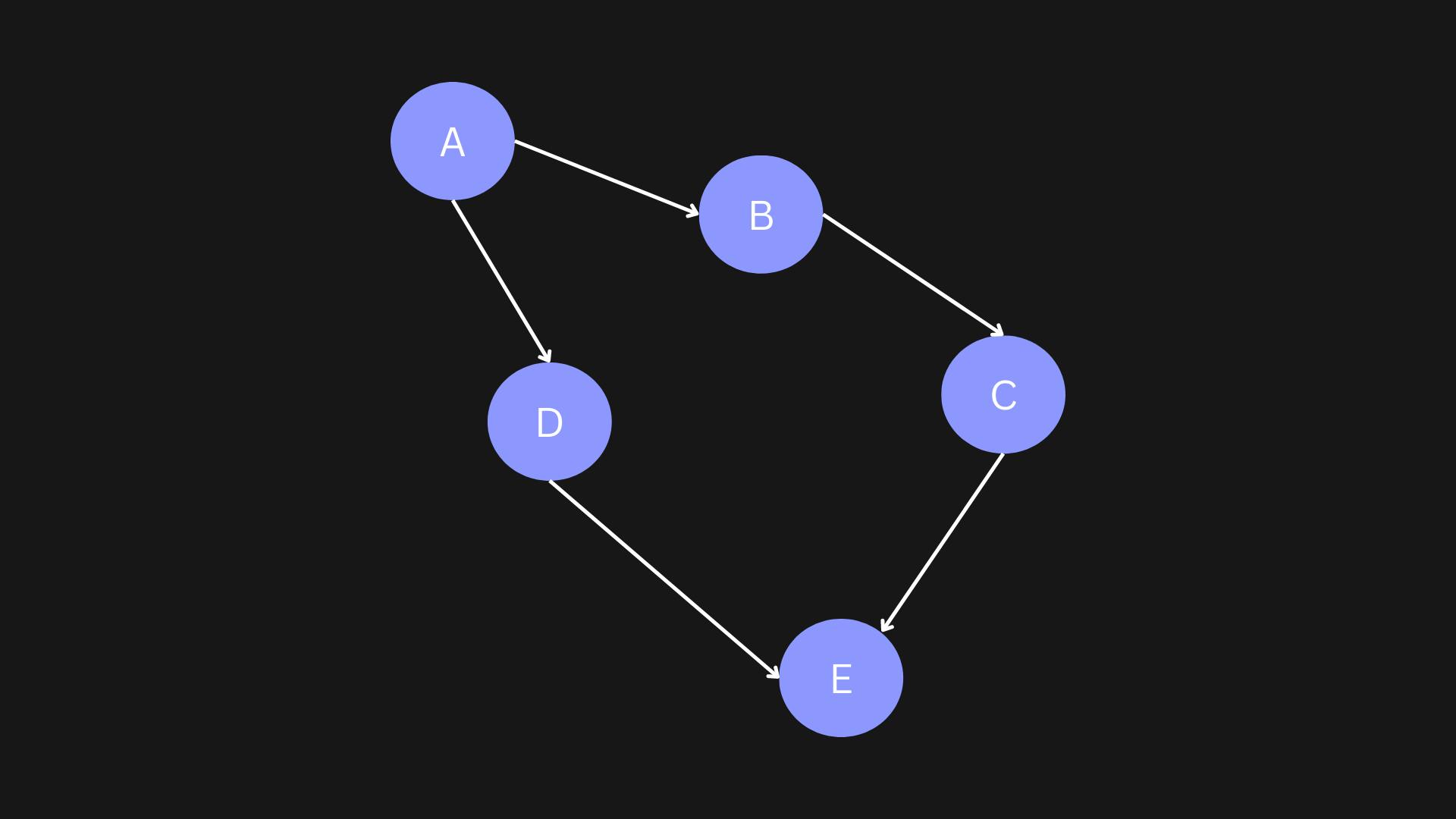
5 points denoting 5 places are marked over here named A, B, C, D, E. The arrows represent the directions.

• If you are at B, you can move to C only.

• You can't move back to A. If you are at D, you can only move to E, not any other place.

Now, let's say you want to move from A to E. You have 2 paths to go from A to E: One via B (let's call it Path 1) and other via D (let's call it Path 2).

Considering that equal distances are present between any 2 points, it is clear that you would move using Path 2 cuz' it will take less energy.

There are some basic elements of AI that you need to know:

Elements of AI | 01

Agent: It is an entity that acts upon a given environment. In this case, since you are walking from A to E, so you are the agent.

State: It is the environment in which the agent is present. In this case, the network of the 5 places, is the state.

Initial State: It is the initial environment from where the agent starts. Here, if you are standing at point A, it is the initial state.

Actions: It is the set of choices that can be made in a given state. If you are at B, the set of actions will contain just one action i.e {move from B to C} . If you are at A, the set of actions will contain 2 actions i.e {move from A to B, move from A to D} .

ACTIONS(state) -> returns a set of actions that can be performed in a given state

Now, after you perform an action in a given state, your state has changed. So, the computer must have something to determine the state change. Here's where a Transition Model comes into light.

The Transition Model is a function that returns the result after a particular action is performed in a particular state. It takes in state and action as its arguments.

RESULT(state, action) -> returns the resulting state

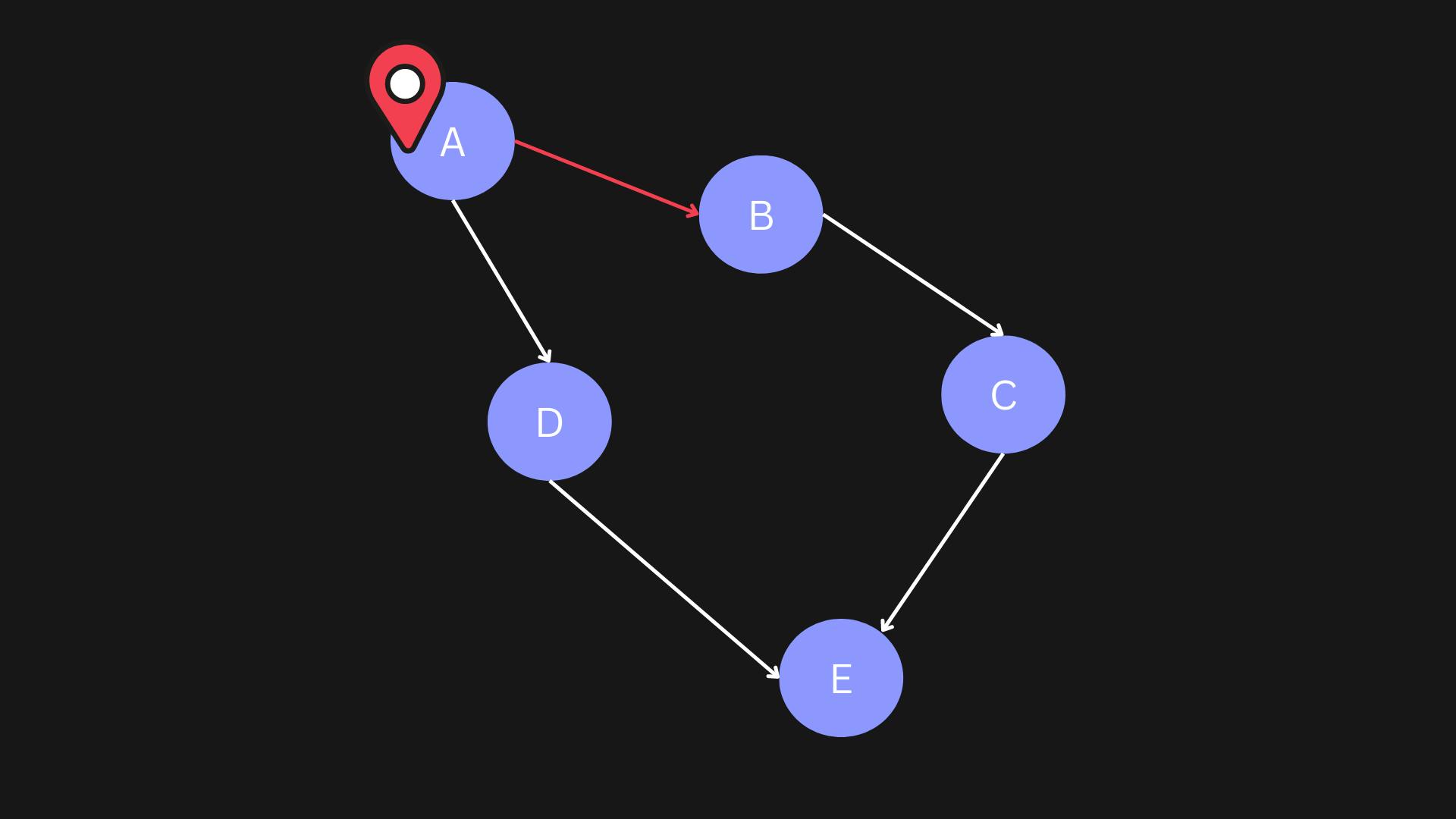
In the picture, you are at point A and you perform an action move from A to B . You will get this resulting state 👇

Now, let's say you have reached your goal. There must be a sort of test to determine that right? As a human, you know that you reached your goal but for a computer, the instruction must be given if it has reached its goal or not. That's why we do a Goal Test to determine if the AI has reached its goal or not.

There were 2 ways to go from A to E, right? But why did you choose the 2nd path? It is because it took less energy. A computer should take the 2nd path so that it takes less computing power. The numerical cost associated with a given path is known as Path Cost.

Now there were 2 set of actions that leads you to the goal. This set of actions that lead the agent to the goal state is called the Solution

The Optimal Solution is the solution with the lowest path cost. In this case, Path 2 is the path with the lowest path cost so it is the Optimal Solution to this problem

So, Search Problems are the problems in which an agent is present which starts from an initial state and the AI finds the Optimal Solution for that agent to reach its goal

Solving Search Problems

In a search problem, data is stored in a node. It is a data structure that holds information that is important to the AI. A node contains:

• A state

• Its parent node: The node through which the current node was generated

• The action: That was applied to the parent to get to the current node

• The path cost from the initial state to this node

Algorithm

1. Start with a frontier containing the initial state and an empty set of explored items

2. REPEAT UNTIL THE GOAL IS REACHED

   • if the frontier is empty:

     • return None as there are no solutions.

   • else:

     • Remove a node from the frontier. We will store this node in a variable (let's say the variable is checking_node) for checking.

     • If the checking_node is the goal then return the solution.

     • else:

       • If the checking_node is not present in the explored set then find all the nodes that can be reached through that node and add them to the frontier.

       • Then add the current node to the explored set.

Removing the node from frontier

The Frontier is just a data structure where nodes get added and removed. But there are choices by which these nodes get removed.

We can either use Stack as the data structure for the Frontier or we can use Queue as a data structure for the frontier. If we are using stack, we will be using breadth-first search on the other hand, if we are using a queue, we will be using depth-first search.

Depth First Search (DFS)

For performing DFS, we treat the frontier as a stack. We add nodes at the last and we remove the last added node from the frontier.

The paragraph written below is taken form: https://cs50.harvard.edu/ai/2020/notes/0/

Take a situation where you are looking for your keys. In a depth-first search approach, if you choose to start with searching in your pants, you’d first go through every single pocket, emptying each pocket and going through the contents carefully. You will stop searching in your pants and start searching elsewhere only once you will have completely exhausted the search in every single pocket of your pants.

Breadth First Search (BFS)

For using BFS, we treat the frontier as a queue. We add nodes at the last and we remove the 1st node that was previously added.

The paragraph written below is taken form: https://cs50.harvard.edu/ai/2020/notes/0/

Suppose you are in a situation where you are looking for your keys. In this case, if you start with your pants, you will look in your right pocket. After this, instead of looking at your left pocket, you will take a look in one drawer. Then on the table. And so on, in every location, you can think of. Only after you will have exhausted all the locations will you go back to your pants and search in the next pocket.

Conclusion

There are more kinds of search algorithms like Greedy Breadth First Search and A* search. In the next article, we will look at Adversarial Search